Adaptateur Tension : Donne les Résistances d'un Pont

[Bud Spencer]

Donc, on connait Vin, Vout et R1 et on veut trouver R2.

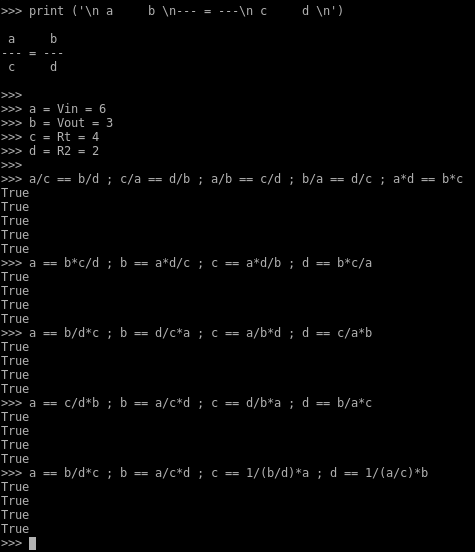
Ça, c’est le premier probleme que tu as rencontré dans ton programme. Tu voulais utiliser le rapport Vin/Vout, mais tu t’es rendu compte que ça foirait suivant si vin/vout <> vout/vin. Malin, tu as donc réécrit 2 fois quasiment la meme chose en conditionnant. Ça, c’était évitable puisque c’est purement mathématique. On sait faire ou on ne sait pas, mais c’est faisable. Je n’ai pas la prétention d’etre un matheux, mais pour faire mon boulot, je suis bien obligé d’en faire un peu et voilà comment je vois la chose :

Une chose est déjà sure, si tu connais R2, Vin, Vout, tu sais trouver R1 (je l’ai lu précédemment) :
Pour l'équation, Considérons U = Vin/Vout

R1 = (R2 . U) – R2
Facile, et ca tu sais faire. Là où ça coince visiblement, c’est pour trouver R2 à partir R1 et c’est effectivement un poil plus .. Moins facile.
Je te la décompose comme si on était à l’école (d’où je me suis enfuit il y a bientôt 40 ans ...)
Donc on sait que :

R1 = (R2.U)-R2

Ce qui signifie que :

R2.U = R1+R2

Que l’on peut décomposer :

U = (R1+R2)/R2 = (R1/R2)+(R2/R2) = (R1/R2)+1

Pour arriver à :

U -1 = R1/R2

Donc, fatalement, il est évident que :

R2 = R1/(U-1)

(C’est ce que j’adore sur ce forum. 4 pages à batailler à faire une pseudo synthèse de U = RI et 4 lignes pour arriver à x = z/(y-1) en partant de (xy)-x = z …)

Donc premiere étape du programme en python, itérer E12 pour trouver R2 ‘idéal’ à partir de chaque R1 issue de E12, vin et vout:

p1.png (19 Kio) Vu 6078 fois

Ça, c’est fait …

Il reste à voir comment on va trouver la bonne valeur dans la liste de la norme. C’est subtil comme truc, parce qu’il faut bien penser que la valeur R2 peut se trouver en dehors de la liste (< ou > ) … on verra ca demain, si j’ai le temps, mais promis, 5 ou 6 lignes de code devraient suffire

[Bud Spencer]

On a trouvé la valeur théorique de R2 et ce que l’on veut maintenant, c’est trouver la valeur normalisée la plus proche. Comme on risque de le faire souvent et avec différentes listes de valeurs normalisées, le mieu est de créer une fonction ou l’on passera en paramètre : la résistance théorique et la liste.
Une recherche dans une liste en python se fait assez facilement. Soit en utilisant la fonction filter avec une fonction anonyme lambda ou alors par itération.
Si je veux par exemple trouver la valeur juste inférieure à 300 dans la liste E12, je peux soit ecrire :

Code : Tout sélectionner

x = list (filter(lambda x: (x<= r),e))[-1]

ou

Code : Tout sélectionner

x =  [x for x in e if x <= r][-1]

Qui me retournera 270

r est la résistance théorique, e est la liste E12. Ces 2 opérations retourne un tableau qui contient toutes les valeurs inferieure à r et [-1] indique que je prends la dernière valeur dans le tableau. Si je veux la valeur juste supérieur à 300, alors je l’écrirais comme ça :

Code : Tout sélectionner

x = list (filter(lambda x: (x>= r),e))[0]

ou

Code : Tout sélectionner

x =  [x for x in e if x >= r][0]

Cette fois ci, le tableau contient toutes les valeurs supérieures à 300 et je prends la première ([0]) ce qui me retournera 330

Premier problème, J’ai déjà 2 possibilités de résultat. x < r ou x > r . Si je cherche par exemple une résistance pour faire éclairer une led, je devrais prendre la plus élevée. Dans le cas du diviseur cela pourra etre l’une ou l’autre suivant le rapport et le sens du pont puisque j’ai l’impératif de ne pas dépasser la valeur vout de départ. J’ajouterais donc un paramètre ‘smaller’ à ma fonction pour lui préciser si je veux la résistance inferieur ou supérieure. Si je passe true à smaller cela signifiera que je veux la résistance inferieur.

Second problème, la liste E12 ne contient que 12 valeurs.
Si je cherche par exemple la résistance juste avant 50, je ne la trouverais jamais puisque la liste commence à 100 et meme cas si je cherche une valeur supérieure 820.

Encore plus vicelard, si je cherche la valeur juste avant 1500, cela me retournera 820 tout comme que si je cherche la valeur juste avant 5000.
Meme constat si je cherche la résistance supérieure d’un valeur inferieur à 100, cela me retournera 100 à chaque fois.
Je vais donc commencer par appliquer un coef multiplicateur à la recherche pour etre sur de trouver un résultat. Pour que ma fonction soit le plus large possible, je vais lui donner la valeur 0.001 (qui me permettra de trouver des valeurs à partir de 100 x 0.001, soit 0.1) et multiplier par 10 jusqu’à ce que le contenu du tableau multiplié par ce coef contienne une valeur supérieure à la résistance passée en paramètre.

Mais ça laisse encore un gros bug. Si je passe par exemple 8300 en paramètre. Mon multiplicateur qui va etre de 100 me donnera des valeurs de 10000 à 82000 et là, si je cherche la valeur juste inferieur (qui devrait me retourner 8200), elle n’existera pas dans le tableau. Je prends donc ça en considération et si je tombe sur ce cas, il me suffit de repasser sur un tableau divisé par 10.

Voilà ce que ça donne en code python, à l’ancienne, c’est-à-dire sans utiliser filter ni de lambda et avec quelques lignes d’autocontrôle pour tester la fonction.

get_r_norme.png (35.05 Kio) Vu 6066 fois

prochaine étape, ajouter ca au programme précèdent qui défini le pont …

[Bud Spencer]

Et voila Le programme complet pour trouver r2 qui correspond à r1 dans la liste E12 en définissant vin et vout . C’est juste la synthèse des 2 codes précédents.
-trouver r2 idéal à partir de vin,vout et r1
-trouver r2 dans la norme à partir de de r2 idéal
-afficher les résultats
r1 est la résistance itérée de E12, r2i est la résistance théorique pour avoir exactement vout , r2 est la résistance de la norme la plus proche pour s’approcher le plus possible de vout sans dépassement et ur2 est la tension finale au borne de r2

pont.png (47.37 Kio) Vu 6058 fois

[Bud Spencer]

Si on veut plus d’infos, il suffit juste de les calculer en revenant le plus simplement du monde aux fondamentales de la loi d’ohm et de les afficher.

ur1 est la tension au bornes de r1 (en v)
i est le courrant dans le pont (en A)
p1 est la puissance dissipé par r1 (en w)
p2 est la puissance dissipé par r2 (en w)

pont_i_p.png (88.52 Kio) Vu 6057 fois

vala, c'est tout

[MSG]

Bonjour ,

Un seul mot à dire ... "J'adore" !
Mais bon , les ternaires et autres fonctions condensés , c'est pour beaucoup de monde de l'hébreu .

Je suis incapable de faire aussi court , mais bon , je me bat avec mes armes et j'arrive presque toujours à mes fins .
Mes bases en informatique : Basic sinclair (ZX81) d'occase , Qbasic sous dos , un peu de 'C' lors d'une formation et puis c'est tout .
Là , j'essaye de me remettre en selle sur du Python .

Pour info , quand on branche les deux résistance de valeur différente , la tension la plus faible se trouvera toujours aux bornes de la résistance de valeur faible .
D'où la difficulté de recherche des couplages .
Tant que Vout < Vin / 2 , R1 > R2 , il faut donc prendre R2 en dessous .
mais dès que Vout > Vin / 2 , c'est R1 < R2 , il faut donc prendre R1 en dessus pour que ur2 soit en dessous des 3.3V.
Lorsque Vout = Vin / 2 , alors R1 = R2
et comme je cherche à partir de la contrainte de na pas dépasser Vout , forcément c'est pas simple , il faut soit prendre la valeur au dessus ou au dessous de la valeur idéale .
Tu l'as très bien expliqué .


Bon , j'ai bossé entre temps sur un code pour décoder les couleurs lu (écrites en texte) en valeur et encoder une valeur en code couleurs (3 , 4 , 5 et 6 annaux) .
Ça fonctionne , mais c'est un roman !

[MSG]

Aller , un petit bout de code pour convertir les valeur résistances en couleurs .

Code : Tout sélectionner

#!/usr/bin/python3

#
# Resistance code couleur - MSG - (c) 03/2020
#
code = (('noir',     1e0, 20e-2, 200 ),\
        ('marron',   1e1,  1e-2, 100 ),\
        ('rouge',    1e2,  2e-2,  50 ),\
        ('orange',   1e3,    '',  15 ),\
        ('jaune',    1e4,    '',  25 ),\
        ('vert',     1e5, 50e-4,  '' ),\
        ('bleu',     1e6, 25e-4,  10 ),\
        ('violet',   1e7, 10e-4,   5 ),\
        ('gris',      '',  5e-4,  '' ),\
        ('blanc',     '',    '',   1 ),\
        ('argent',  1e-2, 10e-2,  '' ),\
        ('or',      1e-1,  5e-2,  '' ))


def couleurs (X) :
    e = 0               # exponentiel
    #
    #  valeur à virgule 
    #
    X = float(X)
    while X < 100 :     # valeur trop petite
        X *= 10         # pousse les chiffres à gauche
        e -= 1          # décrémente exponentiel
    #
    # valeur nombre entier
    #
    X = int(X)            
    while X > 1000 :    # valeur trop grande
        X //= 10        # pousse les chiffres à droite
        e += 1          # incrémente exponentiel
    #
    #  décode le nombre à 3 chiffres
    #
    c1 = int(str(X)[0]) # chiffre centaines
    c2 = int(str(X)[1]) # chiffre disaines
    c3 = int(str(X)[2]) # chiffre Unité
    R = list()  # liste des couleurs 
    R.append( code[c1][0] )         # 1ere couleur - chiffre
    R.append( code[c2][0] )         # 2eme couleur - chiffre
    if c3 != 0 :                    # 3eme couleur ne vaut pas 0
        R.append( code[c3][0] )     # 3eme couleur - chiffre
    else :                          # sinon
        e += 1
    R.append( code [e][0])          # dernière couleur - multiplicateur 
        
    if  e < -2 :
        return ("Impossible , résistance trop petite .")
    elif e > 7 :
        return ("Impossible , résistance trop grande.")
    else :
        return R
    
#
# Main
#



X = input('Valeur de résistance ?\n')
R = couleurs (X)
print ('\nResistance id >  %s\n'  % R)

[Bud Spencer]

Ne t’inquiète pas. Ternaire, lambda, programmation fonctionnelle …, si tu te passionnes un peu pour la programmation moderne, tout ça va venir naturellement. En fait, c’est comme quand tu veux faire quelques choses mais que tu ne sais pas qu’il y a une fonction qui existe déjà pour ça. Donc tu découpes ce que tu veux faire en instructions ‘basic’ conditionnelles et finalement ça marche aussi. C’est juste beaucoup moins rapide, plus long a ecrire et plus long à débugger. Quand tu vas commencer à utiliser ces possibilités, ça deviendra évident et tu n’imagineras plus faire autrement.

C’est aussi un peu pour ça que je ‘ramène ma fraise’ ici. Si personne ne propose un peu de code plus ‘évolué’ pour aider les débutants à en apprendre plus avec des exemples concrets et des explications détaillées plutôt que de les prendre pour des idiots incapables de progresser, alors une rubrique programmation sur un forum comme celui-ci ne servirait à rien.

Pour les couleurs, j’ai juste fait rapidos en c#, mais je vais retranscrire en python et mettre le code ici. Je vois déjà que tu as une approche fondamentalement différente de la mienne (ce qui ne veux pas dire que l’une est mieu que l’autre). Je vais regarder de plus près ton code et l’essayer.

Ps : on a un peu les mêmes origines, j’ai moi aussi commencé sur zx81 et zx spectrum et bien sûr du qbasic, gwbasic, basica en plus de tous ces trucs incontournables de l’époque comme l’asm, c, pascal, fortran ...

[MSG]

Depuis la console Python , j'ai fais un petit test logique pour ceux qui , comme moi , sont ou ont été fâché avec l'apprentissage de la règle de trois (ou de Troie , je sais plus ! ) .
Une relation évidente (entre règle de trois et pont de résistance) pour les mathématiciens , mais pas forcément pour les électriciens campés sur leurs formules .
PS: qu'est-ce qu'elle a bien pu me fait tourner en bourrique , celle-là !



Perso , je me plantais une fois sur deux avec la méthode de la division en premier , puis multiplication ( dite méthode du L ) .
Avec la méthode de multiplication en premier , puis division , ( dite méthode du Z ou du N ) , c'est selon comme on le regarde , je ne me trompe plus !

A méditer !

[MSG]

Bonjour ,

Dans ta démonstration , pour trouver R2 avec la formule R2 = R1 / (U-1)

J'ai une autre façon de faire ...

je dis que le courant i = Vin / (R1+R2) = V1 / R1 = V2 / R2

V2 = Vout
V1 = Vin - Vout ou V1 = Vin - V2
et donc j'isole l'égalité suivante :
V1 / R1 = V2 / R2
qui correspond à ... (voir ci-dessus Règle de trois)
V1 * R2 = V2 * R1
je dis alors que ...
R2 = V2 * R1 / V1
et simplement , je remplace V1 par sa valeur ...
R2 = V2 * R1 / (Vin - V2)
ou ...
R2 = Vout * R1 / (Vin - Vout)

[Bud Spencer]

Tout a fait, ca fonctionne tout pareil. Perso je vais plus directement a une simplification plus radicale parce que j'ai sans doute plus l'habitude, mais ca revient exactement au meme et si tu veux encore simplifier vout * r1 /(vin-vout) tu arriveras forcement à r1/((vin/vout)-1).